|
|
|
Scalars and Vectors:
Scalar quantities:
A scalar quantity is a magnitude (size) value only
E.g. Mass
Temperature
Area
Volume
Vector quantities:
Vector quantities have both size and direction
E.g. Force
Weight
Velocity
Acceleration
Vector quantities can be expressed by arrows whose length represents the magnitude and direction is the direction of the vector quantity.
Adding vectors:
Vectors can be added diagrammatically by placing the vectors head to tail giving a resultant vector from the start of the first to the end of the last.
The best way to show a worked example of how to add vectors is by an example:
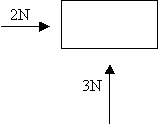 |
The box above has a force of 2 Newtons pushing it left and a force of 3 Newtons pushing it up we can add these forces together
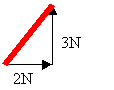 |
The red line is the resultant force we add the two forces by using Pythagoras.
Resultant = √22+32
= √13
= 3.6
We work out the angle of the force by using
trigonometry:
θ = tan-1 1.5
= 56.3°
So vector = 3.61 N at an angle of 56.3° to the
horizon
All vectors can be added in a similar fashion.
Resolving vectors:
Any vector can be resolved into its components. This is shown below:
|
|
V = Vx + Vy
Example:
|
|
Vx = V sin θ
Vy = V cos θ
Vx = 16 sin 30
= 13.86 N
Vy = 16 cos 30
= 8 N